Louis de Broglie

In 1924 Louis de Broglie had argued that particles should have a wavelength associated with them. de Broglie’s theory led to an experiment consisting of a beam of electrons directed at a nickel crystal. The electrons created a diffraction pattern, from the diffraction patten the wavelength of the electrons could be calculated and the calculated value agreed with the value predicted by de Broglie.
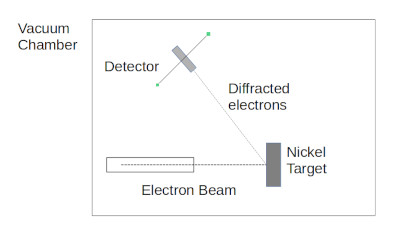
de Broglie scattering experiment
AF DeFerrari all rights reserved.
Confirmation of de Broglie’s prediction brought duality (particle and wave aspects as always coexisting) into the nature of fundamental particles, this led quickly to the development of wave mechanics, or quantum mechanics, by Heisenberg and Schrodinger in 1927.
Werner Heisenburg Erwin Schrodinger

Schrodinger’s equation can be solved for the wave function of a particle. While the wave function itself has no immediate physical significance it can lead to determining the probability of finding the particle at a given time in a given place. Summing all locations yields a probability density function for the particle. This was in stark contrast to the Bohr model.
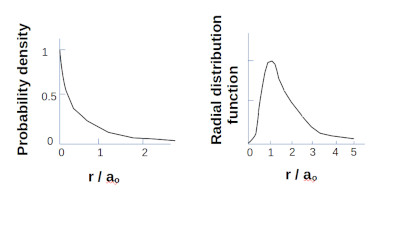
Hydrogen 1S electron probability density and Radial distribution function.
AF DeFerrari all rights reserved.
If we could shrink ourselves and sit on the nucleus of the Bohr atom, we would see the electron moving around the nucleus in a circular orbit having a radius of precisely ao (the Bohr radius).
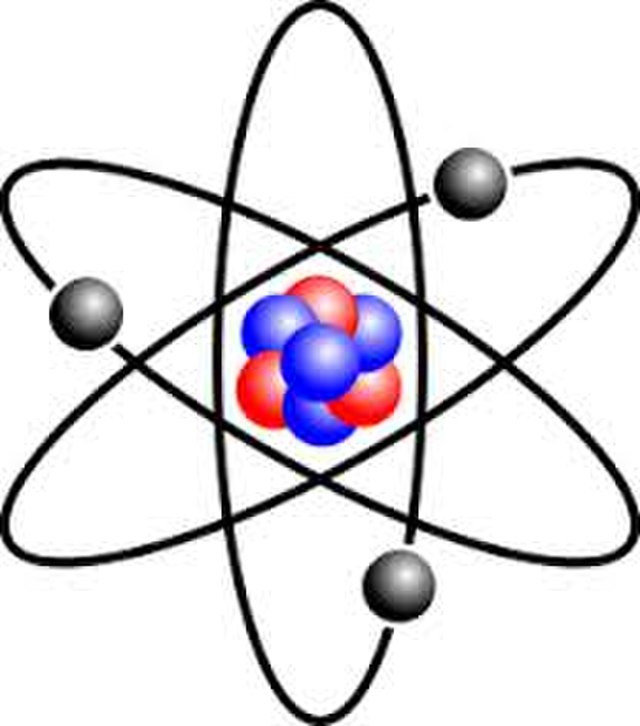
Bohr model of the atom with three electrons
Creative Commons Zero, Public Domain Dedication
Sitting on the nucleus of the Schrodinger atom, we would see a fog of negative charge (assuming our eyes take a “time exposure” of the electron motion). Near the nucleus the density of the fog is high, but if we walk out along a radius, the fog thins out. When we are several atomic diameters away from the nucleus, we look back and see a spherical cloud of negative charge, with the nucleus at the center of the charge.
In the Bohr atom the electron moves like a satellite about a planet; in the Schrodinger atom the electron is smeared out into an electron cloud, much like a puff of cotton candy.
For the hydrogen atom at it’s lowest energy state. QED predicts a finite probability of the electron being found directly in the center of the proton.
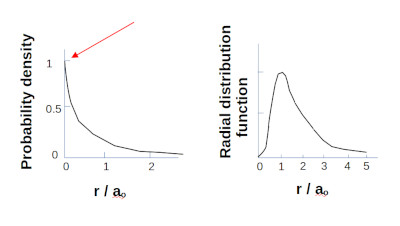
For the Hydrogen 1S electron at lowest energy state there is a probability of finding the electron in the center of the proton.
AF DeFerrari all rights reserved.
But this is not considered a problem in QED because in fact the proton and electron aren’t particles at all, they are waveicles (part particle, part wave). It is the wave nature of the electron and proton that allows one to pass through the other.
When taking into account the volume of space the most likely location to find the electron is one Bohr radius from the nucleus.
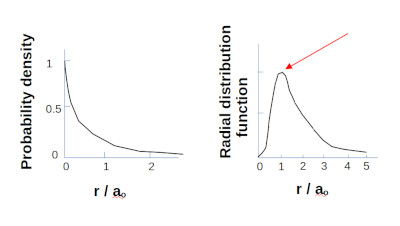
For the Hydrogen 1S electron most probable to find the electron 1 Bohr radius from the proton.
AF DeFerrari all rights reserved.
With QED the location of the electron with respect to the proton is still being accounted for by r (the same r as used in Coulomb’s Law and bringing with it the point charge approximation).