Background for the Hydrogen Atom Solution
Given the boundary condition of a uniform flux density on the surface of the atomic nucleus, the familiar inverse square law equation can no longer be used to calculate the force between a proton and an electron. A solution for the Hydrogen atom has been archived with a modified form of the inverse square law.
As Bob and I began to consider the significance of his discovery we were interested in finding a way to test it's validity.
Bob's mechanical engineering degree obtained in the 1940's gave him a broad exposure to mathematical transformations used to simplify difficult calculations. In addition, during the course of Bob's career he had worked with high frequency circuits and had some experience with the use of a Smith Chart. These two experiences led Bob to believe a modified version of the Smith Chart could be used to solve for the force between a proton and an electron.
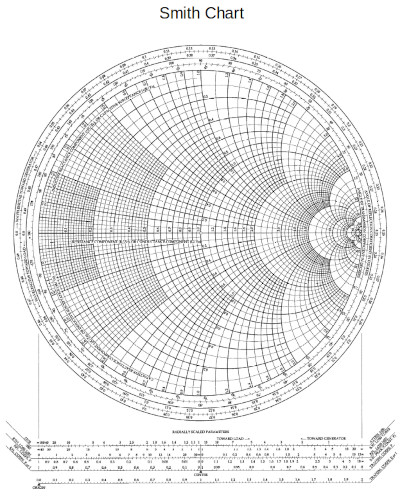
in the public domain
Figure showing a Smith Chart.
With Bob's encouragement I began investigating the smith chart with the intent to see what could be done to solve the hydrogen problem. The figure below shows the scale for a two dimensional space similar to what is used in the Smith Chart.
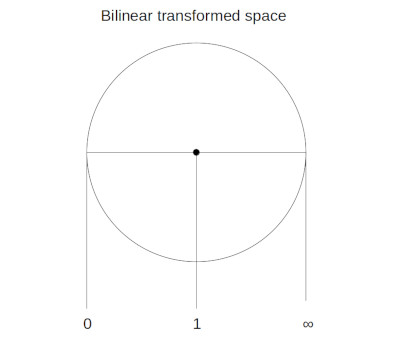
AF DeFerrari all rights reserved.
In our discussions we envisioned a stereoscopic projection of the proton surface onto a plane that was tangent to the proton surface at the point closest to the electron.
AF DeFerrari all rights reserved
Example of a stereoscopic projection
The equation for a stereoscopic projection being:

We then envisioned a bilinear transformation. The bilinear transformation maps the plane over into a circle.
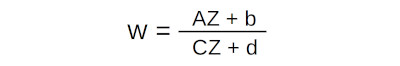
Electronic Applications of the Smith Chart, P.H. Smith, appendix B
General form of a bilinear transformation.
The following figure shows the final transformed space after the bilinear transformation of the proton plane and electron. Since the hydrogen atom exists in three dimensions the transformed space must be considered to be a spherical volume. In this volume the electron is located at the center of the sphere (0.53 Ang. from the surface of the proton) and the proton's charge has been spread onto the inner surface of the sphere.
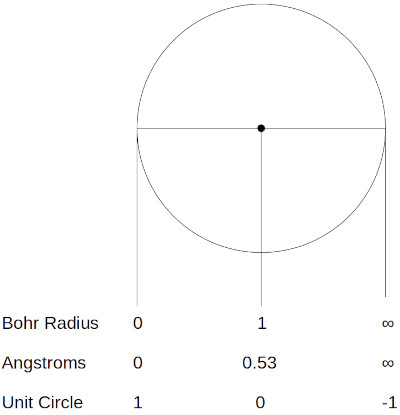
AF DeFerrari all rights reserved
The proton's charge is uniformly distributed on the inner surface of the sphere and is fixed. The electric flux density of the inner surface of the sphere cannot change in response to movement of the electron inside the sphere.
The lines of flux emanate from the inner-surface of the sphere (proton surface) and terminate at the center of the sphere (the electron). In this transformed sphere the spacial coordinates are non-linear, however the electric field lines are linear.
Since the flux density on the surface of the proton is uniform and fixed the amount of electrostatic force pulling the electron to the left (towards the proton) is the same as the amount pulling the electron to the right (away from the proton). The electron is stable at the Bohr radius with only electrostatic force at work. Angular momentum is not required.
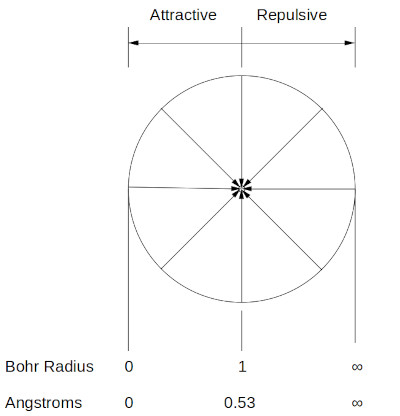
AF DeFerrari all rights reserved
When the electron is at 0.53 ang. the electrostatic forces are balanced.
If the electron is "displaced" to the left toward the proton more electrostatic force will be present to the right of the electron pulling it back toward the center of the transformed space.
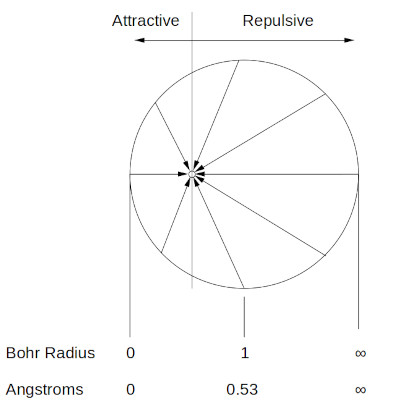
AF DeFerrari all rights reserved
If the electron is displaced toward the proton the repulsive electrostatic force will pull the electron away from the proton.
If the electron was to be "displaced" to the right (away from the proton) the larger amount of attractive electrostatic force to the left of the electron would pull it back towards the Bohr radius.