Mathematical Solution for the Hydrogen atom
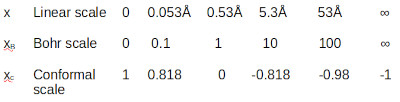
To solve for the force between the proton and electron in the hydrogen atom I started with a linear scale from zero to infinity. Zero representing a point on the proton surface that is closest to the electron. I then scaled the linear scale by dividing by the Bohr radius (xB scale). I then performed Conformal Mapping reflecting a line traveling through the transformed sphere (xc scale).

Note that this scale reflects a unit sphere.
Examples of the resulting scales shown below.
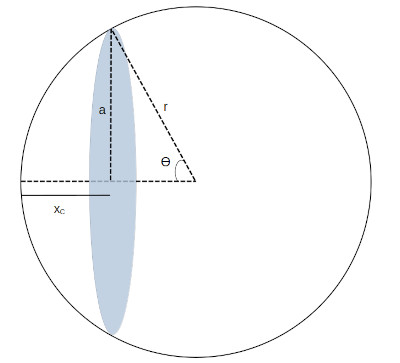
Then using the conformal scale obtained for the unit sphere I calculated the characteristic angle associated with that value.
AF DeFerrari all rights reserved
Equation used to calculate Theta
Using the calculated angle I calculated the volume of the sphere to the left of the x value (attractive volume). Being a unit circle, the radius was equal to 1.
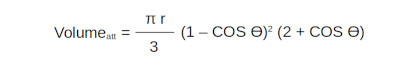
The volume to the right of the x value (repulsive volume) being:
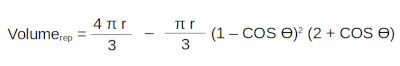
Combining the standard inverse square law with the volume ratios gives the following force equations. They are a modified version of the square law which is not based on the point charge approximation.
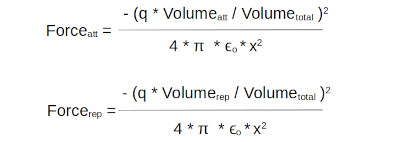
The total force being the attractive force minus the repulsive force.
The total force equation based on the Polata Atomic Model is shown graphed below. Coulombs law is shown for reference. It can be seen that at distances larger than about 6 times the Bohr radius the newly calculated curve matches Coulombs law. At shorter distances the force equation deviates from Coulombs law and predicts a repulsive force between the proton and electron.
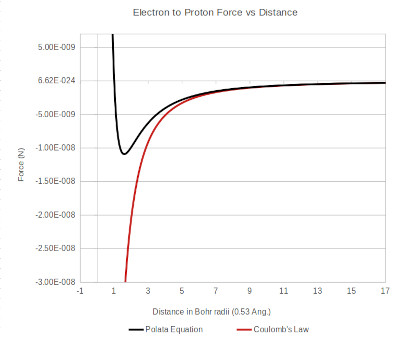
AF DeFerrari all rights reserved
Graphical integration of the force curve based on the Polata Atomic Model yielded an ionization potential of 13.6 ev, closely matching the reported value.
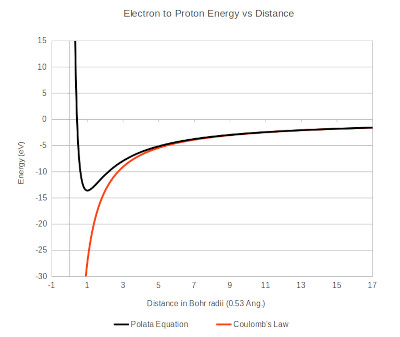
AF DeFerrari all rights reserved
With the Polata Atomic Model angular momentum is not required to prevent the electron from falling into the nucleus of the Hydrogen atom. A fixed electric flux density on the surface of the proton provides both an attractive and repulsive force on the electron.