Mathematical Solution for the Helium Ion (He+)
Back in the early 90’s Bob and I were excited about my results with the hydrogen atom. We wondered how to apply the technique to helium. With two electrons we could not imagine how to place the second electron while we moved the first electron to find the first ionization potential.
We understood we could use the technique for the second ionization potential of helium, but when I went looking I could not find the average electron to nucleus spacing for ionized helium. About that time I had to refocus my attention to my day job, and Bob continued to spend his retirement advocating for his theory.
As I was approaching my retirement, I began to think about Bob’s theory and it occurred to me that in the case of the helium ion I could iterate to determine the spacing of the electron to the ionized helium nucleus. Since the second ionization potential was well known I just had to select an electron to nucleus spacing and calculate the associated ionization potential. Then either increase or decrease the spacing until the ionization potential matched the reported value. I would then have the equivalent of the Bohr radius for ionized helium.
Below is a table of values I calculated to solve for the electron to nucleus spacing for ionized helium. I used the exact same technique as used for the hydrogen atom, with the exception that the charge on the nucleus became two. From the literature the second ionization potential of helium is -54.4 eV.
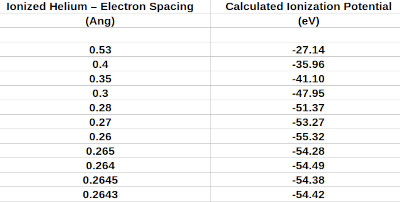
Table showing assumed electron to ionized helium nucleus spacing and calculated second ionization potentials.
As you can see the result I obtained was about 0.264 ang.
Below is a graph showing force as a function of distance calculated using the transformed space technique, Coulombs law is shown for comparison.
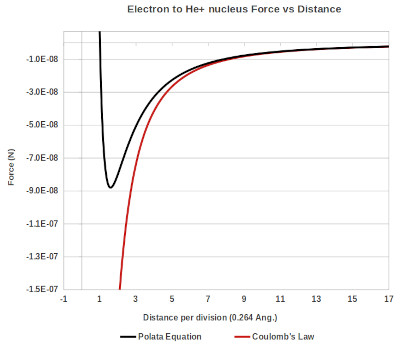
Graph showing the force as a function of distance for the electron to the He+ nucleus.
Below is a graph showing energy as a function of distance calculated using the transformed space technique, Coulombs law is shown for comparison.
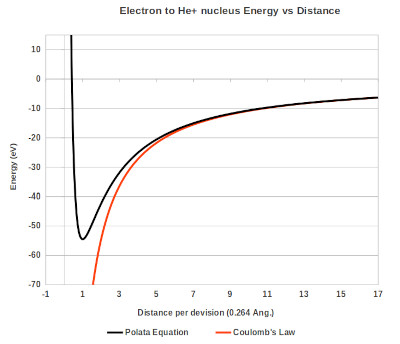
Graph showing the energy as a function of distance for the electron to the He+ nucleus.
My intention was to publish this result and to ask readers to either confirm or disprove this result. As I was preparing my ionized helium web page it occurred to me I should do a bit of searching on the internet to see if over the years this spacing had been published to the net.
The first inquiry I made returned the result that in an ionized helium atom, the most probable distance between the nucleus and the electron is r = 26.5x10-12m.
So again, with no angular momentum, using only electrostatics and assuming the electric field strength on the surface of the nucleus was uniform and fixed, Bob’s theory was able to relate the average electron to nucleus spacing to the ionization potential of an electron. This time for Ionized helium.