Charles de Coulomb

Coulomb’s law was first published in 1785. In it Coulomb describes the electrostatic force between electrically charged particles.
Coulomb’s law predicts the force between charged particles is directly proportional to the scalar multiple of the number of charges and inversely proportional to the square of the distance between them.
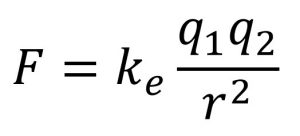
Coulomb's equation
It is the distanced term I would like to draw your attention to. The value r as used in Coulomb’s law is the distance from the center of one charged particle to the center of the other charged particle. This definition was described by Coulomb and has since become known as the point charge approximation.
I would also like to point out that should the value r become zero Coulombs law would predict an infinite force between the charged particles. Of course this would never have been a problem in Coulombs time as his work was done with charged objects that had substantial physical dimensions.
I would also like to point out that Coulombs law works equally well for both insulators and conductors although what is physically happening in the materials is quite different.
In the case of conductors (by which I am referring to mostly metals) charge (or electrons) move freely on the surface of the metal, but the volume inside the metal supports no electric field.
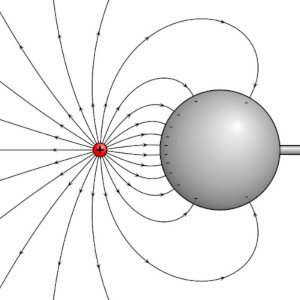
Electric field lines on a conductor
by Creative Commons Attribution-Share Alike 3.0.
In the case of insulators (wood, quartz, most everything that is not metallic) the electrons cannot move about (that’s why they are an insulator), but electric fields can be supported inside insulators. In the case of insulators we use the principle of super position (we assume the charges are randomly distributed, then calculate the effect of each charge and then sum all of the effects together) and just as with conductors we find Coulomb’s law gives an accurate prediction of the force between charged insulators.
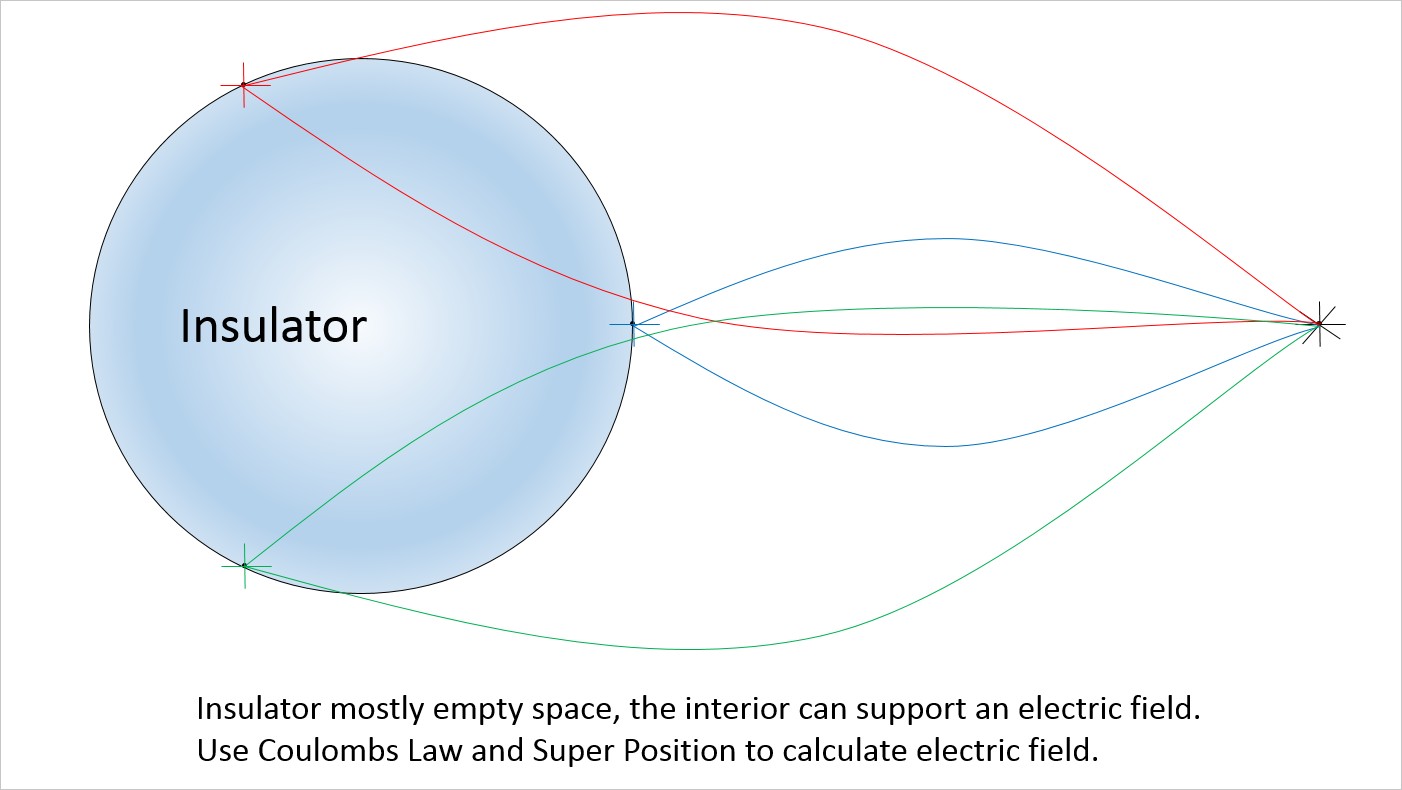
Electric field lines in an insulator
by AF De Ferrari all rights reserved.
That’s pretty cool, one mathematical equation predicts the force between charges for both conductors and insulators when physically what's actually happening isn't really the same, wow.