Bob Polata

While Bohr broke with convention by assuming the atom was not constrained to follow classical physics, Bob has broken with convention by assuming the atom is constrained by classical physics.
By taking on the mantle of classical physics Bob has taken us back to 1911 and Rutherford’s model of the atom. But we don’t have to go back to Rutherford’s time empty handed. We go back with experimental knowledge of the atom not available in Rutherford’s time. That being the size of the proton and electron. The proton is currently known to have a diameter of 1.6 to 1.7×10-15meters.
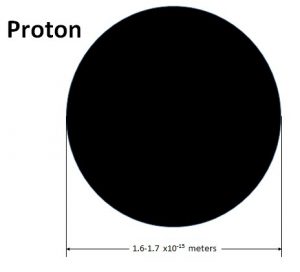
While the electron is a point particle something on the order of 1×10-18meters.
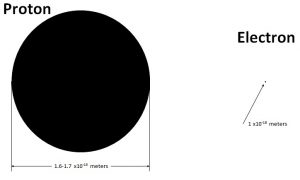
In contrast the Bohr radius Bo is 5.3 x10-11 meters.

What Bob perceived was that the size of the proton was crucial. That is to say while the proton is very very small, it is not a point charge. The underlying assumption to Bob’s theory is that the electric flux density on the surface of the proton is uniform and fixed.
This boundary condition prohibits the use of the point charge approximation on the proton, and as a result Coulomb’s law cannot be applied to the nucleus of the atom or in the case of the Hydrogen atom, a proton.
Polata Atomic Model Assumptions:
1. The electric flux density on the surface of the proton is uniform and fixed.
2. The Proton cannot be treated as a point charge.
3. Coulombs inverse square law cannot be applied to the proton.
During the discussion of Coulomb’s law I took pains to point out that Coulomb’s Law applied to both insulators and conductors. I would now say that the proton does not resemble either. It certainly does not have an excess of electrons capable of redistributing themselves about it’s surface like a conductor.
Creative Commons Attribution-Share Alike 3.0
And with a density many orders of magnitude greater than that of an insulator it is not virtually empty space, capable of supporting an electric field in it’s interior.

So if Coulomb’s Law does apply to the proton, it does so for yet a third mechanism, which may be but for the purposes of exploring the Polata Atomic Model, I am going to say it does not.
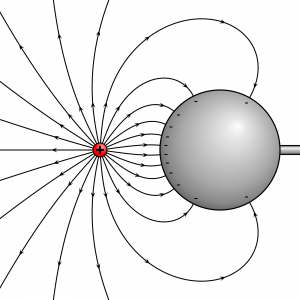
In the Polata atomic model the electric flux density on the surface of the proton is uniform and fixed. A fixed electric flux density on the surface of the nucleus provides an attractive force on an electron when it is beyond equilibrium spacing and a repulsive force when it is closer than equilibrium spacing.
Now that’s a wild concept, the positively charged proton repelling the negatively charged electron with electrostatic force and the more closely the electron approaches the proton the more it is repulsed. How can that be? Well the source of the repulsive force is strain in the electric field.
With Coulomb’s Law a positively charged object will always attract a negatively charged object because the flux density on it’s surface is allowed to vary. As the negatively charged object approaches a positively charged object the flux density on it’s surface facing the negative charge becomes stronger while the flux density on the opposite side becomes weaker. This has been understood since Coulomb published his inverse square law in 1785.
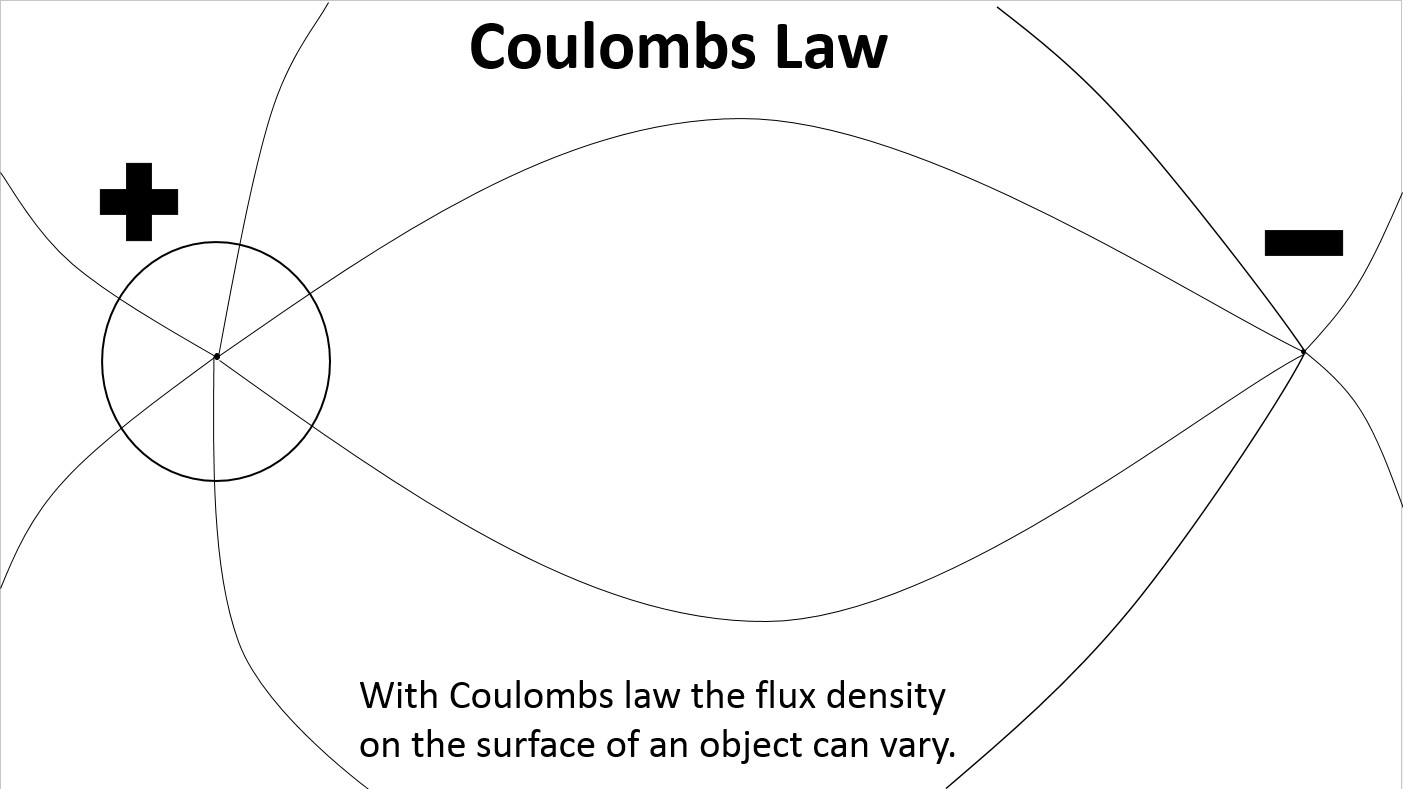
At large spacing the electric field lines on the surface of the proton are evenly distributed.
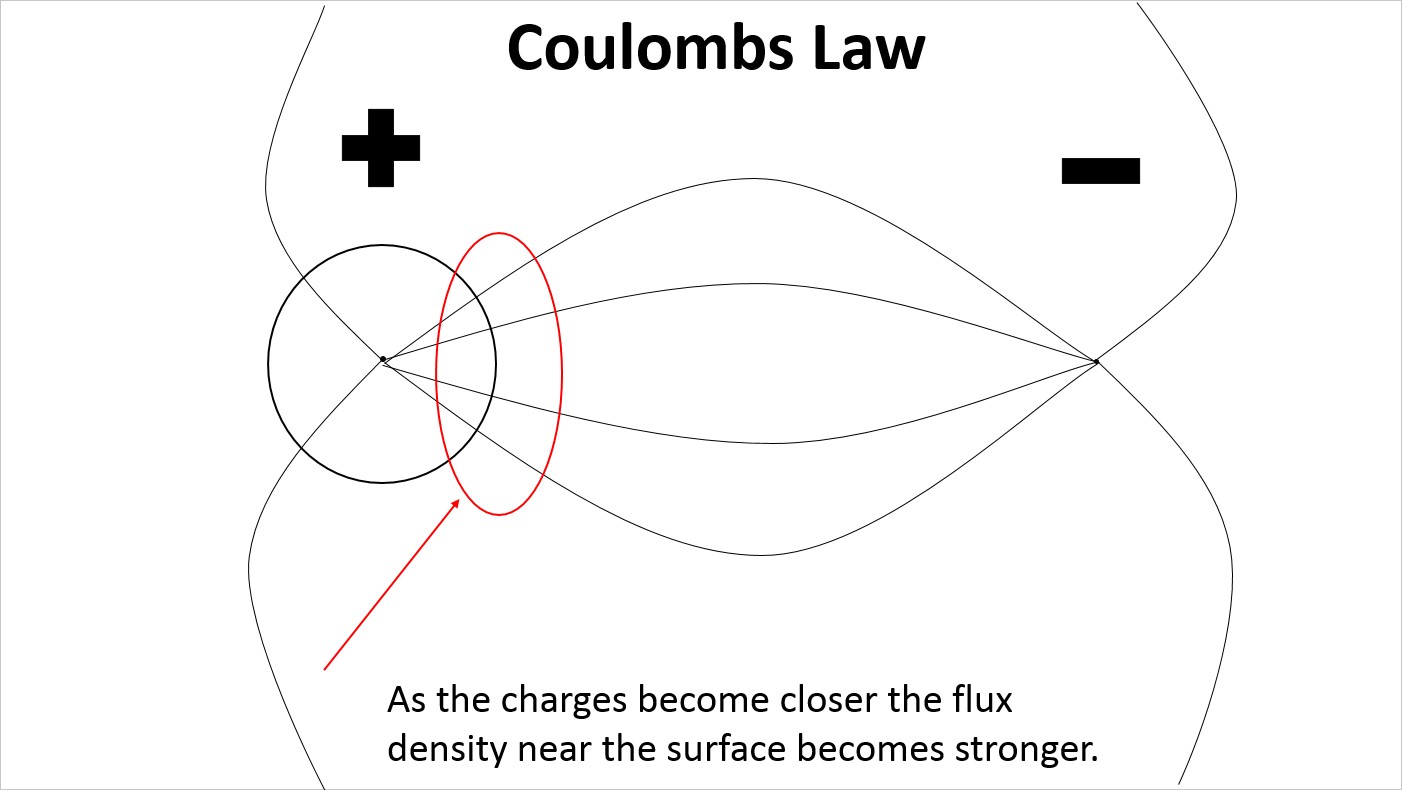
At reduced spacing the electric field lines on the surface of the proton are more densely distributed on the side facing the electron.
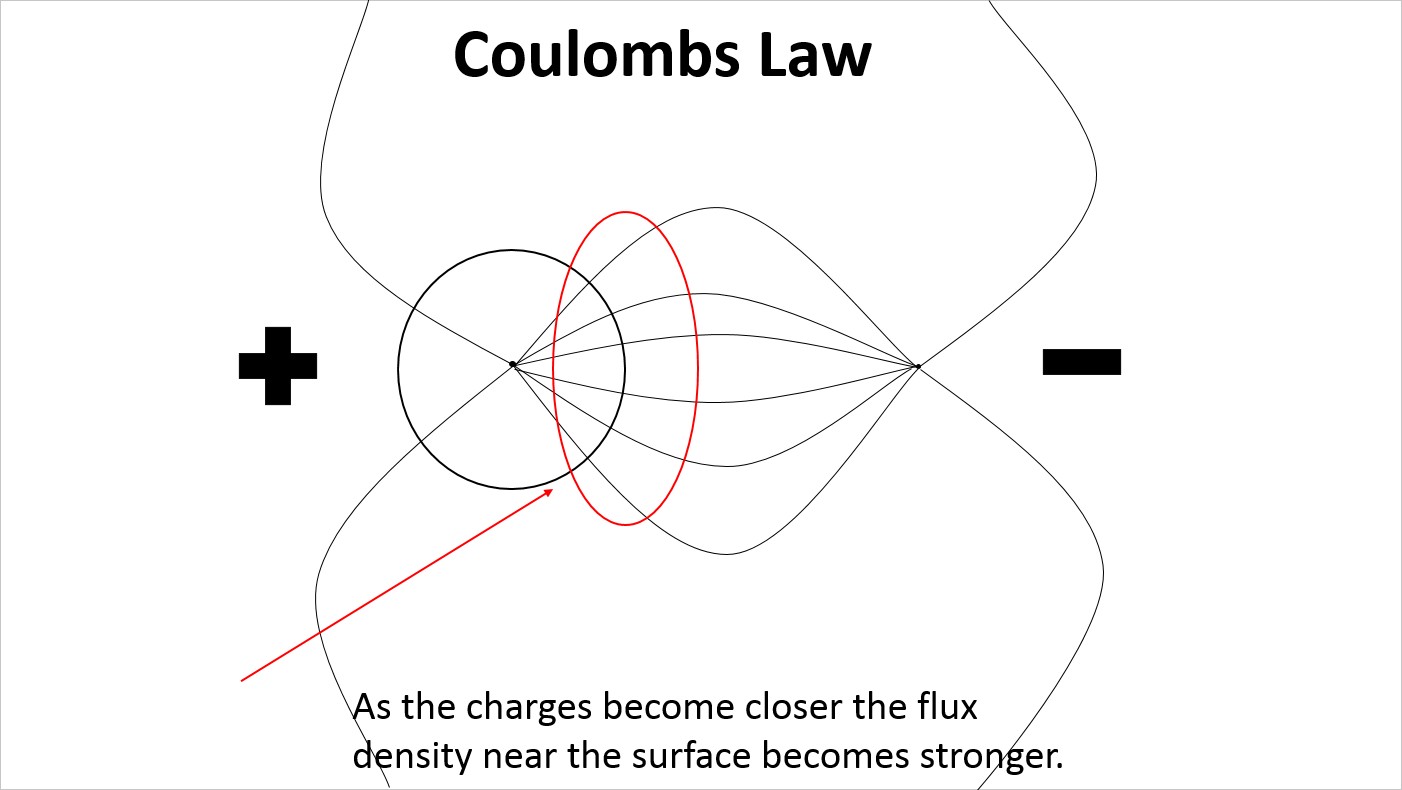
At very reduced spacing the electric field lines on the surface of the proton are very densely distributed on the side facing the electron.
Now if we set the flux density on the surface of the proton as uniform and constant we find that when the electron is far away the flux density follows Coulomb’s law as just described. However as the electron approaches the proton the flux density in space near the proton would like to follow Coulomb’s law and become stronger but it is constrained by the flux density on the surface of the proton which does not change. The constrained flux density near the surface of the proton begins to push back against the electron. The closer the electron gets to the surface of the proton the stronger the constrained flux density near the surface of the proton pushes back against the electron.
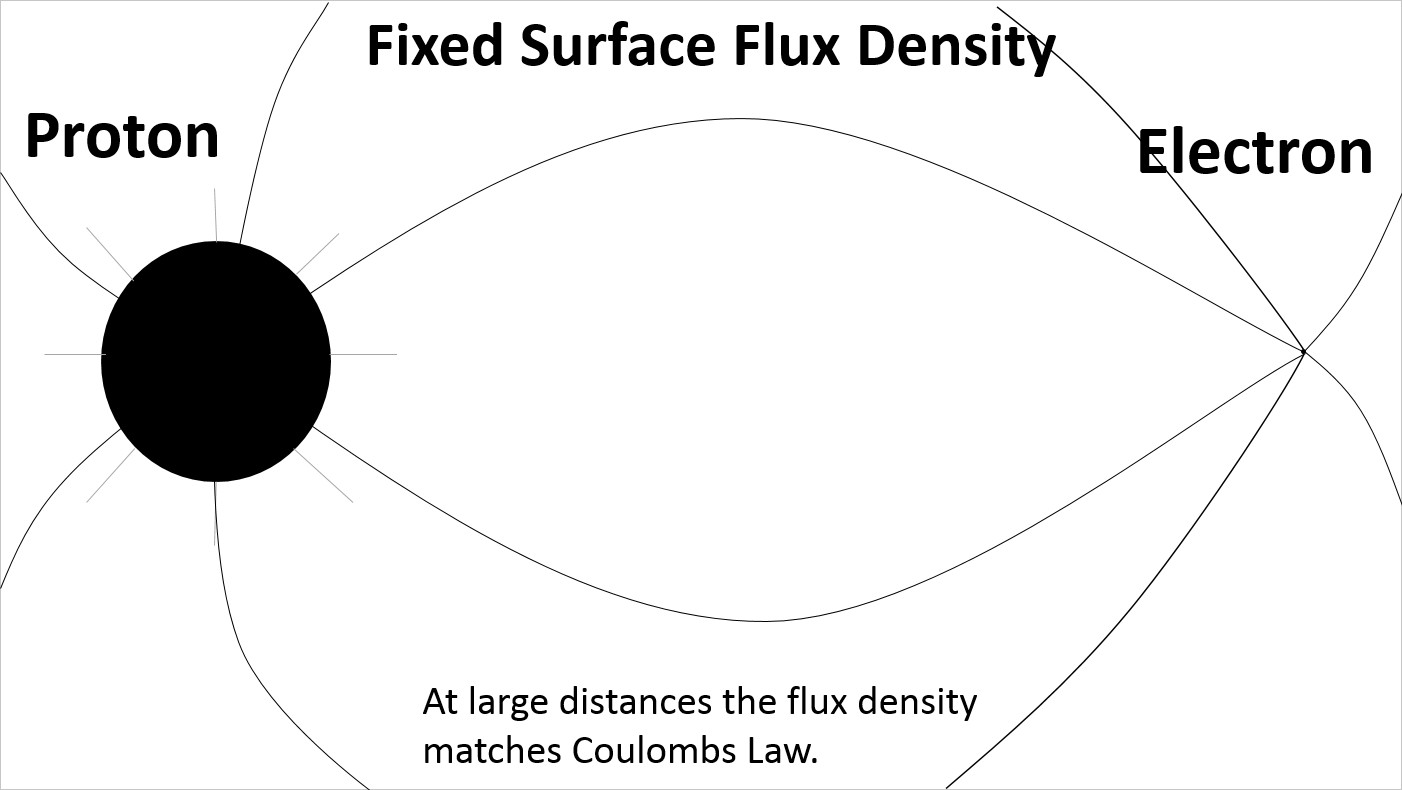
At large spacing the electric field lines on the surface of the proton are evenly distributed.
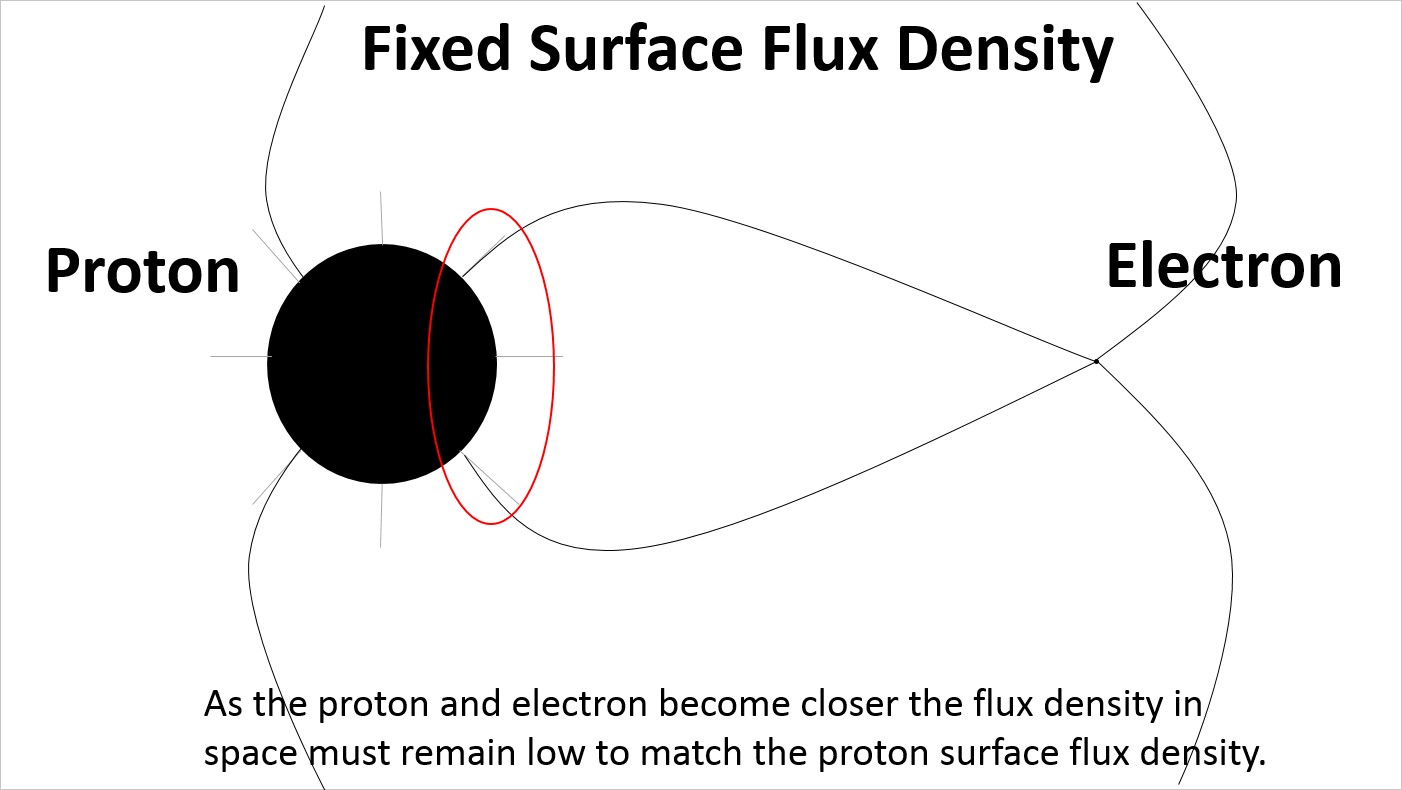
At reduced spacing the electric field lines on the surface of the proton remain evenly distributed creating a strain in the electric field lines extending to the electron.
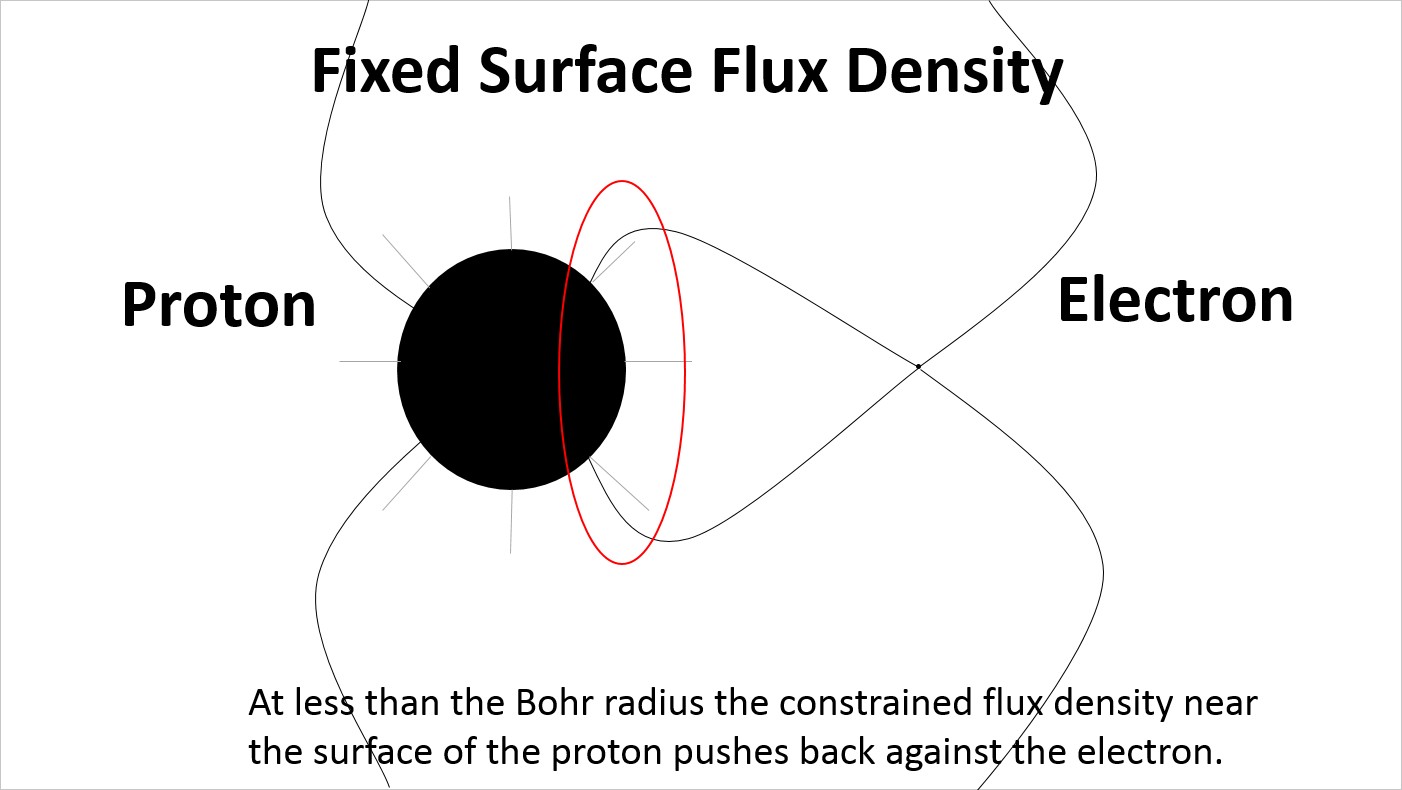
At very reduced spacing the electric field lines on the surface of the proton remain evenly distributed creating a very large strain in the electric field lines extending to the electron.
In the Polata Atomic Model angular momentum is not required to prevent the electron from falling into the nucleus. In the absence of Coulomb’s Law electrostatic force can provide both attractive and repulsive force between positive and negative charges.
In the Polata Atomic Model the atom becomes a system of oscillators. And I would point out that in Bohr’s model of the atom he applied equations developed by Planck for oscillators to determine the energy levels of his stationary states. Perhaps he was not all that far from the mark.
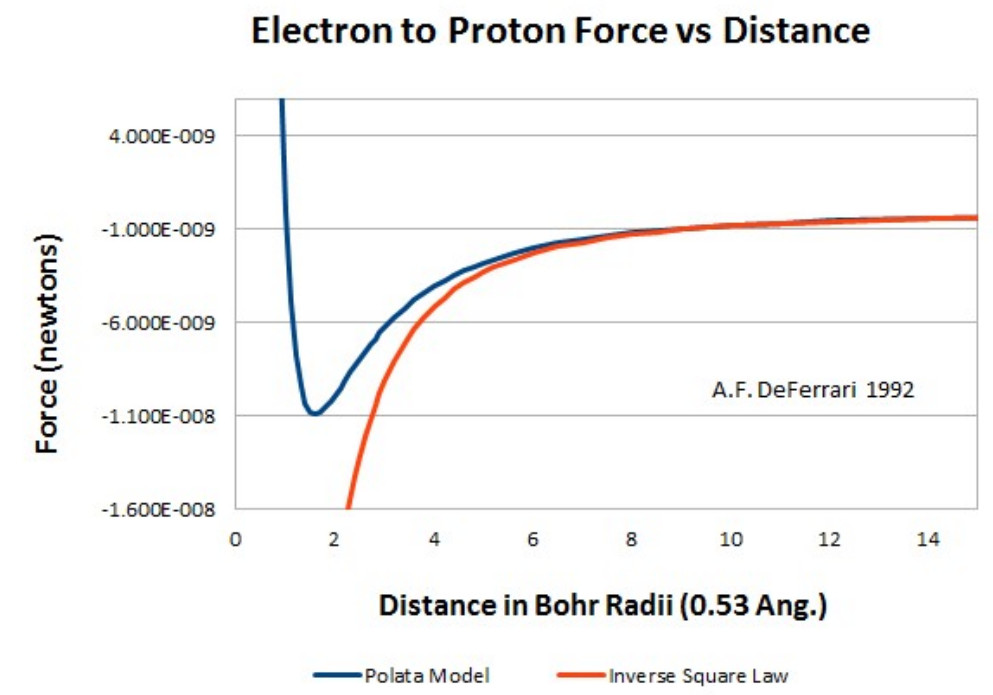
Using the Polata Atomic Model I developed a force equation for the hydrogen atom.
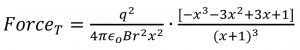
In this force equation the value x represents the distance from the center of the electron to the surface of the proton. The point charge approximation is not applied to the proton. At distances about 5 times greater than the Bohr radius the equation agrees with Coulomb’s Inverse Square Law. At distances less than the Bohr radius it predicts a repulsive force between the proton and the electron.

Electrostatic force between the proton and electron calculated using the Polata Atomic Model.
I graphically integrated the force equation yielding the energy between the electron and proton as a function of distance. Graphical integration of the energy curve yields an ionization potential of 13.66 eV, closely matching the experimental value.
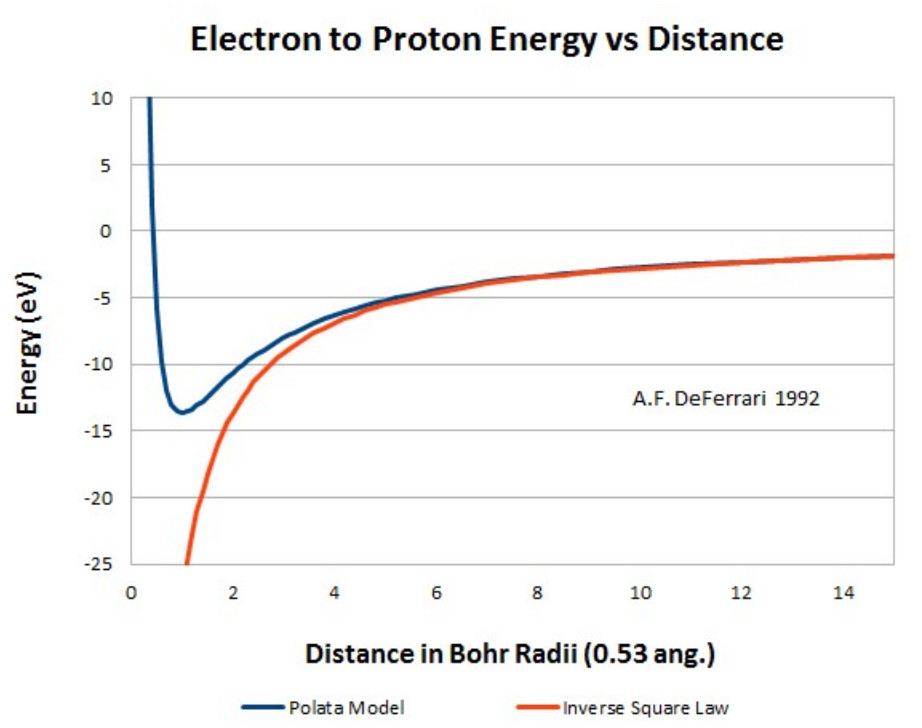
Energy between the proton and electron calculated using the Polata Atomic Model.
So there you have it, a classical model of the atom which is electro-statically stable. Thank you for tuning in and I hope you have enjoyed this discussion.